Teacher Efficacy in Secondary Mathematics: Fostering Confidence and Fluency
Literature Review
Research Question: What practices and school structures create a sense of efficacy in secondary mathematics teachers in order to develop mathematical fluency in students?
There is a call to arms in this nation surrounding the scores of secondary students in mathematics. According to the Programme for International Student Assessment’s (PISA) latest test results in 2012, the United States is 27th among the 34 OECD (Organization for Economic Cooperation and Development) countries, and “performed below average in mathematics” (Gurria, 2014, p.1). President Obama stated in his address at the Third Annual White House Science Fair he is focused on creating an “all-hands-on-deck approach” in areas like math and “we need to make this a priority to train an army of new teachers in these subject areas” (Educate to Innovate, 2013). However, before we begin to analyze the statistics and train teachers in the latest methods to achieve student and national success, let us first define how and what students need to learn in order to know mathematics, or be mathematically fluent. This will then be followed by thoughts on teacher preparedness to facilitate such learning.
Definition of Mathematical Fluency
Stanford University professor George Polya defines mathematical knowledge as a combination of “demonstrative reasoning” and “plausible reasoning.” Demonstrative reasoning is “safe, beyond controversy, and final” or a mastery of skills; plausible reasoning is “hazardous, controversial, and provisional” (Polya, 1954, p. v-vi). Plausible reasoning is how math connects to disciplines like business, science, etc. or making connections to real world experiences. The formulas and processes which students use to present their solutions to an algebra problem are demonstrative in nature; but in order to know what theorems or steps to take was the result of plausible reasoning, or guessing. Polya further goes on to reflect, “…a serious student of mathematics...must learn demonstrative reasoning… yet for real success, he must also learn plausible reasoning; this is the kind of reasoning on which his creative work will depend” (1954, p. vi).
Though Polya’s thoughts were written in the 1950s, his research is echoed by leading mathematics education researchers today (there is still a course - Math 193: Polya Problem Solving Seminar - at Stanford). Guershon Harel, mathematics professor and researcher from the University of California San Diego (UCSD), has respectively, very similar definitions of demonstrative and plausible reasoning but uses the terms “Ways of Understanding” (WoU) and “Ways of Thinking” (WoT) (2008, p.8). He defines knowledge of mathematics as a union of these two sets.
Harel has also written many papers regarding the pedagogy of mathematics including his theory of DNR or DNR-based instruction for mathematics. The D, N, and R respectively stand for duality, necessity, and repeated reasoning (2008, p. 3). Duality posits students only develop ways of thinking when constructing ways of understanding, and these ways of understanding are determined by the ways of thinking they possess. In other words, students gain insights into the purpose of mathematics by investigating the formulas and procedures of mathematics. The necessity principle refers to the idea students must have an intellectual need to learn. The last principle, repeated reasoning, states students need to have repeated experience or practice to gather and retain the ways of understanding and thinking. (Harel, 2008, pp.19-21). Again, Harel contends providing intellectual need, or “utilizing humans’ remarkable capacity to be puzzled” (2008a, p. 488) must be of utmost importance.
These researchers and many others have outlined the components needed for deeper learning in mathematics as ways of doing and knowing mathematics, combined with an intellectual need or purpose for the math being studied. Again, a deeper learning emphasis is not solely on mastering the content, but also on gaining the skills needed to be able to use it, share it and extrapolate the learning to new situations. Now we have a basic grasp of how students should learn, the conversation moves on to what they should learn.
What is the Impact of Standards
In 2009, state leaders in government and education came together to promote the development of standards to “ensure all students, regardless of where they live, are graduating high school prepared for college, career, and life” (Common Core). These standards are promoted as providing demonstrative and plausible reasoning, or the combination of acquiring skills with real-world connections. The Common Core State Standards (CCSS) were developed by consulting leading experts, teachers and other standard communities, such as the National Council for Teachers of Mathematics (NCTM). In August of 2010, the state of California adopted these standards for all public education institutions in grades K-12.
However, there is swirling controversy surrounding these standards and their potential effects on learning mathematics. Opponents of the CCSS object the standards are an imposition of federal rights over a state’s rights and lack of evidence the standards will meet the desired goals of improvement (McDonnell & Weatherford, 2013, p.494). Outcomes of the effects of the CCSS are currently unknown as inaugural testing is commencing in the 2014-2015 school year. Teacher support for the initiative is also waning due to perceived ties to teacher evaluation systems and restriction of their freedom in the classroom. A report from U.S. News & World Report provided some statistics regarding teacher support:
Supporters have touted a survey conducted by Education Next, an education journal, that last year found 76 percent of teachers were supportive of the standards. But in its 2014 poll, Education Next found opposition had more than tripled, from 12 percent in 2013 to 40 percent in 2014. Now, just 46 percent of teachers say they support the standards. (Bidwell, 2014)
Progressive school educators may translate the idea of following standards as an encroachment to their ability to define curriculum. In attending a recent conference with one of the authors of the CCSS for Mathematics, Phil Daro stated the standards were written as a guide to what mathematical knowledge students should be able to perform, demonstrate an understanding of and transform. However, Daro clearly indicated they were not a guide for “how” to teach these skills and practices of the mind (MFASD, 2014).
Other areas of concern exist surrounding the CCSS and students with learning disabilities, especially those diagnosed with mathematics learning difficulties (MD). Powell et al. researched students with MD and cites the research over the last thirty years has indicated “that students with MD require explicit, systematic instruction” (2013, p.41). Explicit instruction generally involves teacher demonstration of detailed step-by-step instructions along with independent practice. In further addressing the needs of MD students, concern exists surrounding the assessment programs which have been developed to coincide with the CCSS, like the SBAC and PARCC. Powell et al. concluded, “schools may find it necessary to use tracks - or for students with MD, the supplementary instruction required in RTI (Response to Intervention) - to prepare students for Common Core assessments” (2013, p. 46). The idea of tracking is in contradiction to some of the latest theories in the epistemology of learning though this topic is beyond the scope of this research.
Standards and Assessments
Regardless of the controversy surrounding the standards, they are the expected learning outcomes for US students in forty-four states. (Six states have either not adopted or withdrawn support of the standards, Academic Benchmarks). The standards represent a shift from a more traditional view of education as teacher-centered delivery of instruction to a more progressive student-centered approach to education. The SBAC and PARCC have been developed as comprehensive, technology-based assessment systems to measure students' attainment of the CCSS. Testing will commence in the 2014-2015 school year. The National Center for Research for Evaluation, Standards and Student Testing (CRESST) based at UCLA asserts these assessments, “are likely to represent goals for deeper learning, particularly those related to mastering and being able to apply core academic content and cognitive strategies for complex thinking, communication, and problem solving” (Herman & Linn, 2013, p.4).
It is the contention of this research the CCSS and its associated testing measures are shifting towards a focus in deeper learning. Proceeding from this basic understanding of how students should learn and what they will be learning, what are the current theories of how educators should be facilitating learning?
Current Research on Mathematics Pedagogy
Referring back to researcher Harel, he questioned whether guidelines for instructors should have been written alongside the standards to assist educators with the transition (MFASD, 2014). Harel suggested educators are currently more focused on ways of understanding and have lacked providing means for obtaining ways of thinking, “... without targeting ways of thinking, students are unlikely to become independent thinkers when doing mathematics” (2008, p.13). Progressive schools are leading the shift in educating students in the ways of thinking about mathematics but there may be some confusion or angst in educators about the balance between the more traditional methods of “tell, show, practice” and the deeper learning model of “discover, explore, use.” This unrest may also be heightened due to a lack of professional development in shifting to the CCSS. “Educators are unclear about where to focus their instructional efforts, and many school leaders are overwhelmed by trying to lead multiple, major reform efforts and uncertain about where to direct professional development” (ASCD, 2012, p. 12).
During research to create an assessment of mathematics teachers’ pedagogical content knowledge, Hauk et al. (2010) defined the four components of a professional understanding of a discipline as having content, discourse, anticipatory and action knowledge. Content knowledge is the “knowledge of topics, procedures and concepts” and substantiates the idea of teachers possessing demonstrative reasoning (Hauk et al., 2010; Polya, 1954). Possessing discourse knowledge allows one to inquire and communicate in mathematics. The researchers defined anticipatory knowledge as “an awareness of, and responsiveness to, the diverse ways in which learners may engage with content, processes, and concepts” (Hauk et al., 2010, p.3). Action knowledge is the ability to differentiate instruction based on students’ needs and the ability to enact the previous three components while teaching. It appears whether one is a teacher or a student, the possession of plausible reasoning or ways of thinking about mathematics (Polya, 1954, Harel, 2008) is essential. An interesting result of their research was that professional development (their subjects participated in 80-100 hours of PD over the course of a year) provided a significant improvement in knowledge, particularly discourse knowledge (Hauk et al., 2010, p. 14). So given this model for what teachers should know and be able to do, what practices help foster a sense of being able to enact the model?
Teacher Efficacy
Anita Woolfolk Hoy, a preeminent researcher in teacher efficacy, stated, “Teachers who set high goals, who persist, who try another strategy when one approach is found wanting—in other words, teachers who have a high sense of efficacy and act on it—are more likely to have students who learn” (Shaughnessy, 2004). A teacher’s sense of efficacy, or the perception of having an effect on student learning, has been researched for the last forty years. Hoy, and fellow researcher Rhonda Spero, also suggests “some of the most powerful influences on the development of teacher efficacy are mastery experiences during student teaching and the induction year” (2005, p. 343). Thus, “the first years of teaching could be critical to the long-term development of teacher efficacy.” Not only could they be critical, but it could be their last formative experience unless meaningful professional development is provided. Dylan William, Emeritus Professor of Educational Assessment at the University of London’s Institute of Education, discusses this phenomenon, “People make claims about having 20 years’ experience, but they really just have one year’s experience repeated 20 times” (Leslie, 2015).
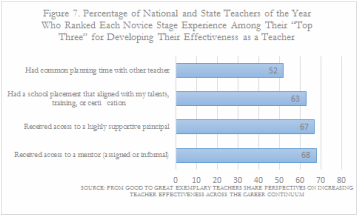
Teacher and education researcher Doug Lemov wrote a book, Teach Like a Champion, about effective teaching techniques. He spent years observing teachers and capturing their “best moves.” Lemov’s claim is good teaching doesn’t just happen, it needs to be coached and practiced. He equates it with witnessing seemingly effortless excellence in a sport, but the made free throw or golf shot “is in fact the product of countless hours of practice and analysis” (Lesle, 2015). While some teachers may be “natural educators”, the majority of us need to work at it. Figure 7 shows the top experience of novice teachers for developing their effectiveness as a teacher was having access to a mentor. This study comes from the National Network of State Teachers of the Year (NNSTOY) and the Center on Great Teachers and Leaders (GTL Center) at American Institutes for Research, which conducted surveys on exemplary teachers on increasing teacher effectiveness across their careers (Behrstock-Sherratt et al., 2014).
The implications of teacher efficacy go beyond individual student concerns. Eric Hanushek, a Stanford educator and member of the Hoover Institute, along with fellow researcher Steven Riskin, have reviewed and conducted studies on the impact of teacher effectiveness on the economy and other policy matters. While the statistics and calculations are above the scope of this paper, their findings clearly state teacher effectiveness has an impact on individual student’s future earnings; and cumulatively the effect of replacing only 5% to 8% of the U.S.’s most ineffective teachers could quadruple our gross domestic product (Hanushek & Rivkin, 2012). However, they also concluded determining the characteristics of effective teachers is an area for continued study.
Efficacy and Inclusion
Teacher efficacy can also be impacted by the wide range of student learning styles and needs, including those of special education needs (SEN) students. Special education needs (SEN) students are generally supported jointly by teachers and other SEN or inclusion personnel. However, support of SEN students is primarily attributed to the classroom teacher. Research conducted on teachers’ attitudes towards inclusion, perceived adequacy of support, and the classroom learning environment found, “Teachers attitudes towards inclusion increased with greater perceived adequacy of internal and external support” (Monsen et al., 2013, p.1).
Researchers Hobbs & Westling wrote about their experiences in conducting a course instructing both general and special educators in best practices in inclusive education. One of the main components of their course focused on building “an emphasis on cooperative learning and team decision making” (2002, p. 188). This idea of collaborative effort between general and special educators was found to be imperative for successful inclusion to incur as found by researchers Broderick and Vakil et al. as reported by Monsen et al. (2013, p. 124). Hobbs & Westling also discuss the need for general and special educators to be trained as partners and collaborators as a “cooperative venture” in the education of SEN students (2002, p. 188). One of the strategies Hobbs & Westling used to improve collaboration was the use of “in vivo” or real-life cases both types of educators brought to the class to investigate. The participants of the class stated the cases were an “irreplaceable component to the class” (Hobbs & Westling, 2002, p. 192). This area of learning for teachers around the needs of SEN students is another component to consider when evaluating a teacher’s sense of individual efficacy.
Back to Deeper Learning
From early progressive educational theorist John Dewey to current researchers Guershon Harel and others, the answer to how deeper learning occurs has not changed. Students and teachers need to be engaged in lessons and assessments which challenge them to such activities as thinking critically, justifying their reasoning, and communicating their findings. Deeper learning organizations have shown improvement in students’ learning of mathematics (at least according to standardized tests). One of these organizations is the Silicon Valley Mathematics Initiative (SVMI). SVMI’s work is in providing professional development, establishing content-focused coaching in schools, and collaboratively examining student work to inform teachers of pupils’ understandings to foster teacher efficacy and students’ deeper learning of mathematics. After their first decade of work with teachers they found, “...when teachers teach to the big ideas, participate in ongoing content-based professional development, receive support in the classroom from well-trained coaches, and use specific assessment information to inform instruction, their students will learn and achieve more” (Foster & Noyce, 2004, p. 11). The questions remain as to why there is an ongoing necessity of instructional coaches for mathematics teachers? As the literature and my research has uncovered, the following factors have been shown to affect the teaching and learning of mathematics:
- Degrees earned or the years of teaching experience do not necessarily matter when forming teacher efficacy.
- Teacher efficacy does have an impact on student learning.
- Teacher efficacy is best fostered by employing a community approach in both defining common mathematical practices, the use of mentors and/or other instructional coaches, and peer learning.
Based on the review of literature spanning almost a century it is the claim of this paper for students to gain mathematical fluency they need to develop both habits of thinking and understanding. Students also need to practice those habits immersed in environments which provide real-world context and a need to learn. Teachers need a sense of efficacy to be able to foster this type of learning and facilitate the desired results of students, parents, universities, and future employers, regardless of the subject area.
